Computer Algorithm - Tree Data Structure
Computer Algorithm - Tree Data
Structure
One of the most important data storage and organizing methods of computer algorithms is the tree, which is one of the non-linear data structures. In general, a tree structure refers to the "branched" relationship between different parts or nodes of a tree, as seen in the case of a natural tree.
In the language of the book it can be defined as a finite set of one or more nodes. Suppose such a set or tree is T, then
A) This tree should have a special node which will be identified as the root of the tree and it will be called root (T).
B) The nodes other than this root are divided into n≥0 number of disjoint sets, respectively T_1… .T_n, etc., each of which reappears one by one with the characteristics of a new tree. These T_1… .T_n trees are called root sub-trees.
Mathematically: T = {r 〖〖UT _1 〖UT〗 _2U…. 〖UT〗 _n
It is expressed as T = {r, 〖T〗 _1, T_2,…, T_n for easy understanding.
Notice that this recently given definition of a tree is just a recursive or repetitive ঃ a tree is defined as the sum of many trees. Fortunately, we do not have to read in infinite repetition or recursion, because each tree has zero number of sub-trees and a single tree can have zero number of sub-trees (h = 0) as a basis. Although it is possible to give a non-recursive definition of a tree, this definition is quite self-contained. Even the trees that can be seen in nature can be thought of in this way. From the buds of new trees, but also the sub-trees that have their own buds sprouted.
By definition, the smallest tree is a tree that has only root nodes. For example, a tree like Ta = A. When it comes to multiple nodes, the rest of the nodes are split into subtree. For example, Tb = {B, {C}} is a tree consisting of a root node E and a subtree {C. Finally, the following set and a tree
Tc = {D, {E, {F}}, {G, {H, {I}}, {J, {K}, {L}}, {M}}
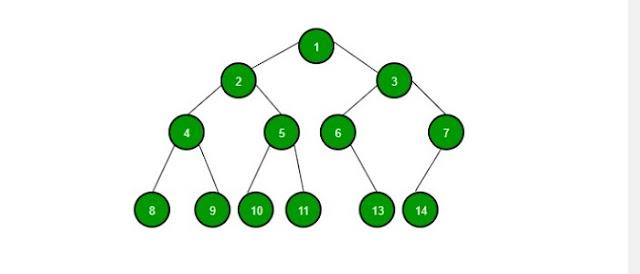
But looking at this strange thing, it doesn't seem to be anything like a tree at all. In fact, it is expressed in pictures like the picture below
Only in the palm of the hand can one find harmony with the tree. Using this recursive method to express such a tree j = {r, T_1, T_2,…, T_n ঃ graphically: First we draw the root node r. Then draw the sub-trees T_1, T_2,…, T_n one by one below the root. Finally we draw a line from the root to the sub tree.
However, exposing the tree in this way gives the opposite image of a real tree. But this is how the tree is expressed in the data structure. And in the discussion of trees, the words "up" and the actual "down" are considered subject to this figure. For example, when we go from the root of a tree to a sub-tree, we say we are going down a tree.
Some definitions
Consider T = {r, 〖T〗 _1, T_2,…, T_n} where n≥0 is given as the definition of a tree.
>> The degree of the node (fabmatbab) is the number of sub-trees connected to this node. Example The degree of the tree above is n.
>> The node that has no sub tree has zero degree and it is called Leaf.
>> The root ri of the i-th sub tree 〖T〗 _i is the child of the root r of the tree. Grandchild can be defined in the same way.
>> Again, the root node of tree T is called the parent of all sub-trees. Similarly, grandparents can be defined.
>> The two separate sub-trees i-th and j-th of tree T 〖T〗 _i and 〖T〗 _j are called siblings respectively.
What is clear from these definitions is that they are a curious combination of mathematical, humanistic, and plant words. There are other terms that are important to know before discussing them. Path and path length: If a tree with a set of nodes R is given, its ear is a path P is the combination of how many nodes P = {,…, k}! Where ri for every i-th (1 d ”id” k) node is a component of the set R (riXR), and the i-th node ri is (i + 1) - the father of the node (ri + 1) ). The path -0 length of this path P is k + 1.
Notice for example a tree Tc in the picture above. This tree has many different paths. In fact, if you listen properly, you will see that this tree has 29 different paths. These include zero path-length path {D}, one path-length path {E, F}, and three path-length paths {D, G, J, K.
Some more definitions
Consider a tree with one set of nodes R according to the above definition:
>> The level or depth of a node ri (riXR) is the length of a path unique from the root r of tree T to ri. For example, the root of tree T is at level zero, and the roots of its sub-tree are at level one.
>> The height of a node ri (riXR) is the maximum distance from a node ri to a leaf. So the leaves are all at zero height.
>> The height of a tree is the height of its root node r.
>> Consider two nodes ri and rj. ri is said to be an antecedent of rj if a path from ri to rj is present. Notice that ri and rj can be but the same node. That is, a node is its own predecessor. However, a suitable pre-male is said to be present when a path is present up to ri and rj whose path-length is one or more.
>> In the same way, node ri is called the north male of rj if a path from ri to rj is present. Since ri and rj can be the same node, a node is its own answer male. A suitable answer is called a male when there is a path from ri to rj whose path-length is one or more.
There are different types of tree data structures. Among them
> N-ary Tree
> Binary Tree
> Binomial Tree
> General Tree
> M-way search Tree
> AVL search Tree> B-Tree
Considering the scarcity and importance of space in the magazine, only Binary Tree is discussed in detail here.
Binary Tree:
A binary or binary tree is a tree that has only two branches or sub trees.
Binary tree is a finite set of nodes which have the following characteristics:
1. Either set is an empty set, T = 0
2. Otherwise the set contains a root r and two separate binary trees TL and TR, T = {r, TL, TR.
Here tree TL is called the right subtree of tree T.
The binary tree is considered as an ornamental tree in almost all cases. Consider the two binary trees in the figure below. Each tree has a root and a single non-empty tree. In one case the left-subdivision is not empty, in another case the right-subdivision is not empty. Since decoration or order is important, these trees are two but separate trees.
From some tree-related sources, it is evident that a tree with ne ”0 number of E. Turnal nodes has n + 1 number of external nodes.
It can also be proved that a binary tree of he ”0 height can have a maximum of 2h + 1-1 number of E. Turnal nodes. In reverse, it is also possible to prove that the number of E. Turnal nodes characteristic of a tree is at least EMBED Equation.3.
Finally, a binary tree of he ”0 height can have a maximum of 2h leaves. Conversely, the height of a tree with a number of leaves is at least EMBED Equation.3.
Evidence of all these sources could not be given here as it is beyond the scope of this article. If necessary, you can see in the following book.
Tree traversal:
The tree has different applications. Thus different types of algorithms are used for tree use. However, a common feature of different types of tree algorithms is to visit each node of the tree in a certain way. That is, the algorithm continues to navigate the tree data structure and perform a single computation on each node. The whole business of this journey is called tree traversal.
There are two types of tree navigation - single-distance-first-traversal and deep-first-traversal. Notable among the several types of depth-first traversal are: preorder traversal, inorder traversal, and postorder traversal.
The following tricks will be used in the next discussion: T = {A, B, 0, C, 0,0}}, {D, {E, {F, 0,0}, {G.0,0}, H, {1,0,0}, {0}}}
Pre-order Traversal:
We will consider pre-order traversal as the first depth-first traversal method. For binary trees:
1. The first route must be visited; Then
2. The left sub-tree must travel; And
3. Finally you have to travel to the right sub tree.
For example, the pre-order traversal in the image above yields the following output: A, B, C, D, E, F, G, H, I
Post-Order Traversal:
We will consider post-order traversal as the second deepest-first traversal method. For binary trees:
1. Must travel left sub tree first; Then
2. Must travel to the right sub tree; And
3. Finally you have to visit the route.
For example, the post-order traversal in the image above yields the following output:
C, B, F, G, E, I, D, A
In-Order Traversal (Regular Decoration Tour):
We will consider in-order traversal as the third depth-first traversal method. For binary trees:
1. Must travel left sub tree first; Then
2. Route must visit; And
3. Finally have to travel to the right sub tree;
For example, the in-order traversal in the figure above results in the following output:
B, C, A, F, E, G, D, I, H
Although it was appropriate to use the recursive definition in the case of deepest-first traversal, the non-recursive definition is more appropriate in the case of breadth-first traversal. Broadth First Traversal first visits all nodes of zero path-length, then visits all nodes of a single path-length, thus moving forward. At every depth it moves from left to right.
For example, the breadth first traversal in the image above gives the following output:
A, B, D, C, E, H, F, G, I.
Apply the tree:
In different ways, the tree can be expressed using different features of different programming languages. Personally I use Tree as part of a much larger design pattern created in C ++, Java and C Sharp. This type of pattern is not at all suitable for programming contests. It is better to try to solve the problem without applying the original tree. Here I will give the implementation of a tree in C plus plus. But I will try to tell you how to use the original tree concept while discussing various issues. The source code given here is a part of my main object oriented library which is slightly different for publication in magazines. Although the original library was tested on Visual C Plus Plus, Borland C Plus Plus and GNU C Plus Plus, the version published here has only been tested on Visual C Plus Plus and Borland C Plus Plus.
Visitor Class:
The job of this class is to visit different nodes and do some computing. The visit function of this clock is used during different tree traversing. Again, since there are three types of depth-first traversal, this class has been extended to pre-post visitors, and inherited three classes called pre-order, post-order, in-order. . The printing-visitor class prints it as an output during the node visit.
Save this code in a file called Visitor.
/ * Visitor.h file * /
template
class Visitor
{
public:
virtual void Visit (T &) = 0;
virtual bool IsDone () const
{return false; }
};
template
class BinaryTree;
template
class PrePostVisitor: public Visitor
{
public:
virtual void PreVisit (BinaryTree &)
virtual void Visit (T &) {
virtual void Visit (BinaryTree &)
virtual void PostVisit (BinaryTree &)
};
template
class PreOrder: public PrePostVisitor
{
Visitor & visitor;
public:
PreOrder (Visitor & v): visitor (v)
{}
void PreVisit (BinaryTree & object)
visitor.Visit (object.Key ()); }
};
template
class InOrder: public PrePostVisitor
{
Visitor & visitor;
public:
InOrder (Visitor & v): visitor (v)
{}
void Visit (BinaryTree & object)
visitor.Visit (object.Key ()); }
};
template
class PostOrder: public PrePostVisitor
{
Visitor & visitor;
public:
PostOrder (Visitor & v): visitor (v)
{}
void PostVisit (BinaryTree & object)
visitor.Visit (object.Key ()); }
};
template
class PrintingVisitor: public Visitor
{
ostream & stream;
bool comma;
string seperator;
public:
PrintingVisitor (ostream & s): stream (s), comma (false), seperator (",")
{}
PrintingVisitor (ostream & s, string & sep): stream (s), comma (false), seperator (sep)
{}
void Visit (T & object)
{
if (comma)
stream << seperator;
stream << object;
comma = true;
}
void Reset (string str = ",")
{
comma = false;
seperator = str;
}
};
Binary Tree Class:
This is the original binary tree class. See how the root and left and right subtree are used. Various tri-traversals have also been implemented. Additionally, if a binary-tree is given inorder and postorder traversal or inorder and pre-order traversal, there are two functions for preparing a tree using them.
/* BinaryTree.h / template class BinaryTree { protected: T key;
BinaryTree* left;
BinaryTree* right;
public:
BinaryTree ();
BinaryTree (T&);
~BinaryTree ();
void Purge ();
T& Key () const;
BinaryTree& Subtree
(unsigned int) const;
bool IsEmpty () const;
bool IsLeaf () const ;
unsigned int Degree () const ;
int Height () const;
virtual void AttachKey (T&);
virtual T& DetachKey ();
virtual BinaryTree& Left () const;
virtual BinaryTree& Right () const;
virtual void AttachLeft (BinaryTree&);
virtual void AttachRight (BinaryTree&);
virtual BinaryTree& DetachLeft ();
virtual BinaryTree& DetachRight ();
void SetKey(T&);
void DepthFirstTraversal
(PrePostVisitor&) const;
void BreadthFirstTraversal
(Visitor&) const;
int CompareTo (
BinaryTree <T> const&) const ;
void ConstructFromInPost (
vector<T>::iterator,
vector<T>::iterator,
vector<T>::iterator,
vector<T>::iterator);
void ConstructFromInPre (
vector<T>::iterator,
vector<T>::iterator,
vector<T>::iterator,
vector<T>::iterator);
};
template
BinaryTree::BinaryTree () :
key (0),
left (0),
right (0)
{}
template
BinaryTree::BinaryTree (T& _key) :
key (&_key),
left (new BinaryTree ()),
right (new BinaryTree ())
{}
template
void BinaryTree::Purge ()
{
if (!IsEmpty ())
{
delete key;
delete left;
delete right;
key = 0;
left = 0;
right = 0;
}
}
template
BinaryTree::~BinaryTree ()
{ Purge (); }
template
void BinaryTree::AttachKey (T& arg)
{
if (!IsEmpty ())
return;
key = &arg;
left = new BinaryTree ();
right = new BinaryTree ();
}
template
T& BinaryTree::DetachKey ()
{
if (!IsLeaf ())
return *new T;
T& result = *key;
delete left;
delete right;
key = 0;
left = 0;
right = 0;
return result;
}
template
T& BinaryTree::Key () const
{ return *key; }
template
BinaryTree& BinaryTree::Subtree (
unsigned int i) const
{
if (IsEmpty () || i>1)
return *new BinaryTree;
return *(i==0?left:right);
}
template
bool BinaryTree::IsEmpty () const
{ return key==0; }
template
bool BinaryTree::IsLeaf () const
{ return (!IsEmpty() &&
left->IsEmpty () && right->IsEmpty ()); }
template
unsigned int BinaryTree::Degree () const
{ return IsEmpty() ? 0 : 2; }
template
int BinaryTree::Height () const
{
if(IsLeaf()) return 1;
int l = left->Height();
int r = right->Height();
return (l>r?l:r) + 1;
}
template
BinaryTree& BinaryTree::Left () const
{ return *left; }
template
BinaryTree& BinaryTree::Right () const
{ return *right; }
template
void BinaryTree::AttachLeft
(BinaryTree& arg)
{ left = &arg; }
template
void BinaryTree::AttachRight
(BinaryTree& arg)
{ right = &arg; }
template
BinaryTree& BinaryTree::DetachLeft ()
{
BinaryTree r = new BinaryTree(left);
left = 0;
return *r;
}
template
BinaryTree& BinaryTree::DetachRight ()
{
BinaryTree *r =
new BinaryTree(*right);
right = 0;
return *r;
}
template
void BinaryTree::SetKey(T& arg)
{ key = &arg; }
template
void BinaryTree::DepthFirstTraversal (
PrePostVisitor& visitor) const
{
if (visitor.IsDone ())
return;
if (!IsEmpty ())
{
BinaryTree& me =
const_cast< BinaryTree& >(this); visitor.PreVisit (me); left->DepthFirstTraversal (visitor); visitor.Visit (me); right->DepthFirstTraversal (visitor); visitor.PostVisit (me); } } template void BinaryTree::BreadthFirstTraversal ( Visitor& visitor) const { deque> que;
if (!IsEmpty ())
que.push_back(
const_cast*>(this));
while (!que.empty () && !visitor.IsDone ())
{
BinaryTree const& head = *que.front();
que.pop_front();
visitor.Visit (head.Key());
for (unsigned int i = 0;
i < head.Degree (); ++i)
{
BinaryTree<T>& child =
head.Subtree (i);
if (!child.IsEmpty ())
que.push_back(&child);
}
}
}
template
int BinaryTree::CompareTo (
BinaryTree const& arg) const
{
if (IsEmpty ())
return arg.IsEmpty () ? 0 : -1;
else if (arg.IsEmpty ())
return 1;
int result;
if (Key () == arg.Key ())
result = Left().CompareTo
(arg.Left ());
if (result == 0)
result = Right().CompareTo
(arg.Right ());
return result;
}
/*
Constructs From
inorder and postorder traversal
NOTE: the calling object is assumed empty tree
/ template void BinaryTree::ConstructFromInPost (vector::iterator inorderstart, vector::iterator inorderend, vector::iterator postorderstart, vector::iterator postorderend) { AttachKey(new T(postorderend)); vector::iterator result; result = find(inorderstart, inorderend,postorderend);
int d1 = result – inorderstart;
int d2 = inorderend – result;
if(d1!=0)
Left().ConstructFromInPost
(inorderstart, result-1,
postorderstart,postorderstart+d1-1);
if(d2!=0)
Right().ConstructFromInPost
(result+1,inorderend,
postorderstart+d1,postorderend-1);
}
/*
Constructs From
inorder and preorder traversal
NOTE: the calling object is assumed empty tree
/ template void BinaryTree::ConstructFromInPre (vector::iterator inorderstart, vector::iterator inorderend, vector::iterator preorderstart, vector::iterator preorderend) { AttachKey(new T(preorderstart)); vector::iterator result; result = find(inorderstart, inorderend,preorderstart);
int d1 = result – inorderstart;
int d2 = inorderend – result;
if(d1!=0)
Left().ConstructFromInPre
(inorderstart, result-1,preorderstart+1,preorderstart+d1);
if(d2!=0)
Right().ConstructFromInPre
(result+1,inorderend,
preorderstart+d1+1,preorderend);
}
A test program:
This time a test program will explain if the tree is OK and how to use it. This test program, like the example above, prepares a tree in two ways, performs different traversing tests, and finally compares the two trees to see if they are equal.
include
include
include
include
include
include
using namespace std;
include “Visitor.h”
include “BinaryTree.h”
int main()
{
cout << “Demostrating tree” << endl; char pre[]= {“ABCDEFGHI”}; char in[]= {“BCAFEGDIH”}; char post[]= {“CBFGEIHDA”}; vector prev;
vector inv;
vector postv;
for(int i=0;i<9;i++) { prev.push_back(pre[i]); inv.push_back(in[i]); postv.push_back(post[i]); } BinaryTree tree1;
tree1.ConstructFromInPre
(inv.begin(),inv.end()-1,
prev.begin(),prev.end()-1);
cout << “Tree1 – constructed \ from preorder and inorder traversal\n”; BinaryTree tree2;
tree2.ConstructFromInPost(
inv.begin(),inv.end()-1,
postv.begin(),postv.end()-1);
cout << “Tree2 – constructed \ from postorder and inorder traversal\n”; PrintingVisitor putv(cout);
PostOrder pv1(putv);
cout << “Postorder traversal on Tree1\n”; tree1.DepthFirstTraversal (pv1); cout << endl; PreOrder pv2(putv);
cout << “Preorder traversal on Tree2\n”; putv.Reset(); tree2.DepthFirstTraversal (pv2); cout << endl; cout << “BFS on Tree1\n”; putv.Reset(); tree1.BreadthFirstTraversal (putv); cout << endl; cout << “BFS on Tree2\n”; putv.Reset(); tree2.BreadthFirstTraversal (putv); cout << endl; int r = tree1.CompareTo(tree2); cout << “Comparing the trees\n”; if(r==0) cout << “Tree1 == Tree2” << endl; else if(r==1) cout << “Tree1 > Tree2” << endl;
else if(r==-1)
cout << “Tree1 < Tree2” << endl;
else
cout << “Error” << endl;
return 0;
}
ACM-Valladolid Binary Tree Problems:
There are a lot of problems with trees, some of which require direct tree algorithms, while others require the ability to use key concepts differently. First of all we will discuss the problems of using binary tree directly. Note that there may be many issues related to binary-tree but have escaped my notice, in which case I would request to be informed of the matter.
The problem is that a tree is like a programming language in which each node will be given an integer, input and a number. The output should be given as the sum of the numbers of each node in the path from the root to the leaf of this tree.
Solution strategy:
The whole tree can be easily inverted recursively. Then during depth-first traversal you have to add the number of nodes per pre-visit and subtract the number of nodes per post visit. Every in-visit must see if it has reached the end of the road, if it has reached the end, we have reached the end of a path. So we have to compare H with the number to see if it is equal.
Common mistakes:
1. If the tree input is not recursive, taking wide input in multiple lines can be quite troublesome.
2. Not being able to take input just like that
3. Do not use 32 bit integers as integers
Solution:
The upper bouts featured two cutaways, for easier access to the higher frets
/* Problem : 112 — Tree Summing */
include
include
include
include
include
include
using namespace std;
include “Visitor.h”
include “BinaryTree.h”
class TreeSummer :
public PrePostVisitor
{
long Sum;
long desired;
bool done;
public:
TreeSummer(long des = 0) :
Sum(0), desired(des),done(false) {}
void PreVisit (BinaryTree& arg)
{ Sum+= arg.Key(); }
void Visit (BinaryTree& arg)
{
if(arg.IsLeaf())
{
if(Sum==desired) done = true;
}
}
void PostVisit (BinaryTree& arg)
{ Sum -= arg.Key(); }
bool IsDone () const
{ return done; }
};
void TreeInput(BinaryTree & arg)
{
char ch;
long* k = new long(0);
scanf(“\n%c”,&ch);
if(scanf(“\n%ld”,k)==1)
{
arg.AttachKey(*k);
TreeInput(arg.Left());
TreeInput(arg.Right());
}
scanf(“\n%c”,&ch);
}
int main()
{
#ifndef ONLINE_JUDGE
















